First Steps in R
R contains a very comprehensive library with statistical functions, including the most common probability distributions:
There are several functions associated to every probability distribution, and they can be accessed adding a prefix to the distribution name:
_______ _______________________________________________________________________
Prefix Meaning
_______ _______________________________________________________________________
d density function
p distribution function (cumulative function)
q inverse of the distribution function (quantile function)
r random generation of numbers following the probability distribution
_______ _______________________________________________________________________
The arguments are obviously different for each associated function. For the Normal Distribution:
> ?Normal
Normal package:stats R Documentation
The Normal Distribution
Description:
Density, distribution function, quantile function and random
generation for the normal distribution with mean equal to ‘mean’
and standard deviation equal to ‘sd’.
Usage:
dnorm(x, mean = 0, sd = 1, log = FALSE)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)
...
It evaluates the density of the normal distribution with mean mean and standard deviation sd in x abscissa. The normal distribution has density
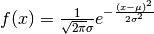
where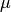 
is the mean of the distribution and 
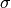the standard deviation.
> x <- seq(-10,10,by=.5) # sequence of numbers
> x
[1] -10.0 -9.5 -9.0 -8.5 -8.0 -7.5 -7.0 -6.5 -6.0 -5.5 -5.0 -4.5
[13] -4.0 -3.5 -3.0 -2.5 -2.0 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5
[25] 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5
[37] 8.0 8.5 9.0 9.5 10.0
> y <- dnorm(x, mean=3, sd=2) # Normal distribution with mean=3 and sd=2
> plot(x,y,main="Normal Distribution Example") # Plot the result
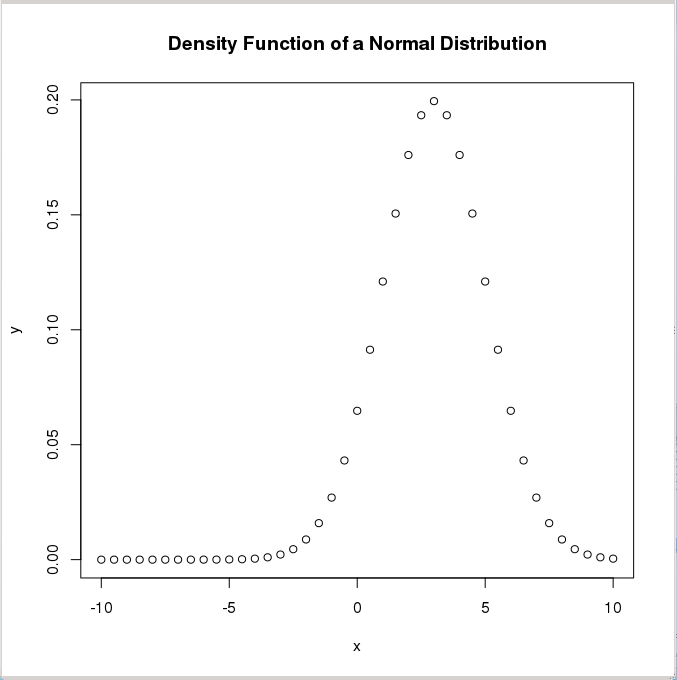
Random sequence of n numbers following a normal distribution with mean mean and standard deviation sd.
> x <- rnorm(1000,mean=3,sd=2) # 1000 random numbers with mean=3 and sd=2
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-3.783 1.694 3.003 3.047 4.436 9.864
> hist(x,main="Normal Distribution Simulation", ylab="Frequency", plot=TRUE)
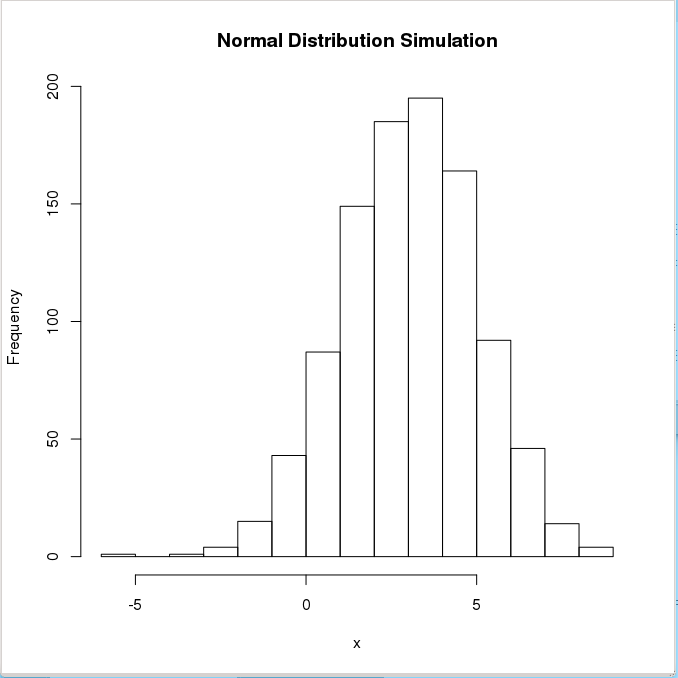
To ensure reproducibility, it is important to set the random number seed when performing simulations:
> set.seed(1000)
> rnorm(10)
[1] -0.44577826 -1.20585657 0.04112631 0.63938841 -0.78655436 -0.38548930
[7] -0.47586788 0.71975069 -0.01850562 -1.37311776
> rnorm(10)
[1] -0.98242783 -0.55448870 0.12138119 -0.12087232 -1.33604105 0.17005748
[7] 0.15507872 0.02493187 -2.04658541 0.21315411
> set.seed(1000)
> rnorm(10)
[1] -0.44577826 -1.20585657 0.04112631 0.63938841 -0.78655436 -0.38548930
[7] -0.47586788 0.71975069 -0.01850562 -1.37311776
It evaluates the distribution function (area below the probability distribution) for a normal distribution with
mean mean and standard deviation sd. By default, lower.tail = TRUE returns the area in the left wing of
the distribution (![P[X \le x]](_images/math/05aeb3b799c221b84b7c1a35f613b89b03574aed.png)
) and lower.tail = FALSE returns the right wing (![P[X > x]](_images/math/f333a452ce0b9cca7ca7340aef56ce7b5fb48f66.png)
).
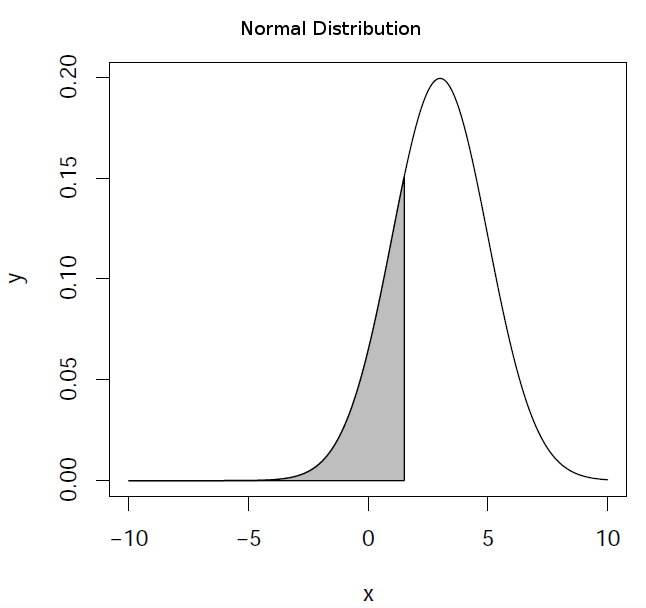
> pnorm(1.5,mean=3,sd=2) # left wing (default)
[1] 0.2266274
> pnorm(1.5,mean=3,sd=2,lower.tail=FALSE) # right wing
[1] 0.7733726
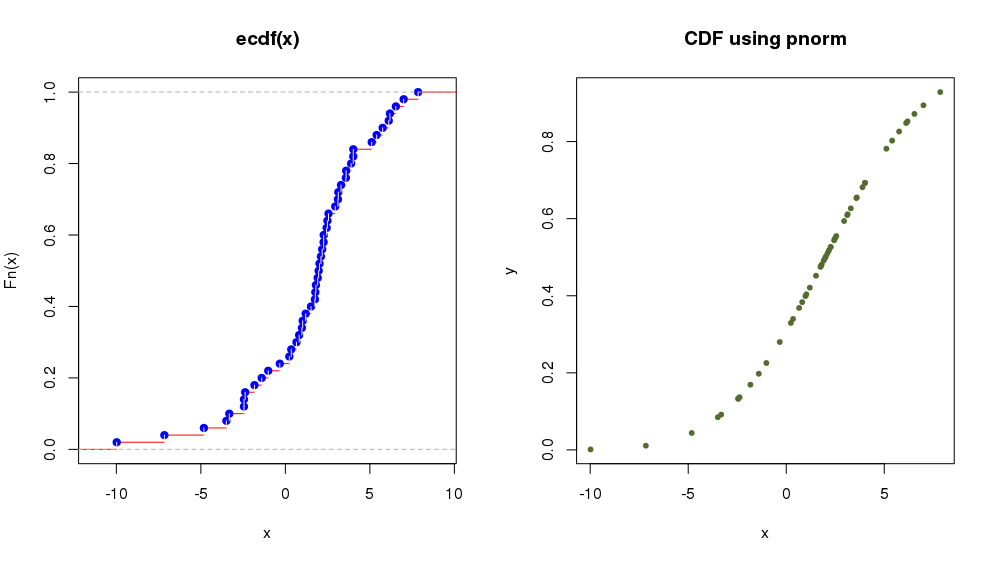
The R object ecdf(x) lets us calculate and plot the Empirical Cumulative Distribution Function (useful when the cumulative distribution is not known). Let’s see with an example how to plot the cumulative function in the case of a normal distribution:
> par(mfrow = c(1, 2)) # define 1 row and 2 columns to plot
> x <- rnorm(50, 2, 4) # random numbers following normal distribution
> plot(ecdf(x),verticals = TRUE, col.points = "blue",
+ col.hor = "red", col.vert = "bisque") # plot Empirical Cumulative Distribution Function
which is equivalent to:
> y <- pnorm(x, 2, 4)
> plot(x,y, main="CDF using pnorm",
+ col="darkolivegreen",pch=20) # plot Cumulative Distribution Function using 'pnorm'
It evaluates the inverse of the distribution function (the abscissa for an area p under the probability distribution) for a normal distribution with mean mean and standard deviation sd. By default, lower.tail = TRUE assumes that the area is that of the left wing of the distribution and lower.tail = FALSE assumes that is the right wing area.
> qnorm(0.2266274,mean=3,sd=2) # left wing (default)
[1] 1.5
> qnorm(0.7733726,mean=3,sd=2,lower.tail=FALSE) # right wing
[1] 1.5
______________________________________________________________________________
Distribution Associated Function
______________________________________________________________________________
Uniform dunif, punif, qunif, runif
Binomial dbinom, pbinom, qbinom, rbinom
Poisson dpois, ppois, qpois, rpois
... d..., p..., q..., r...
______________________________________________________________________________
Normal dnorm, pnorm, qnorm, rnorm
t de Student dt, pt, qt, rt
chi dchisq, pchisq, qchisq, rchisq
F de Fisher df, pf, qf, rf
... d..., p..., q..., r...
______________________________________________________________________________
Purpose: Estimation of the value of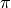 
using random points generated inside a square.
Procedure: Calculate the ratio between the inner and outer points in a circle with radius equal to 1, inscribed in a square of side equal to 2 (i.e., the circle’s diameter is equal to the square’s side).
We save the script in a file called pirandom.R:
# estimate PI by using random numbers
# A.squ = n = (2*r)²
# A.cir = n.inside = pi * r²
#
# pi = n.inside/ r² = 4*n.inside/n
#
pirandom <- function(n) # define function
{
x <- runif(n,-1,1) # random numbers in [-1,1]
y <- runif(n,-1,1) # random numbers in [-1,1]
plot(x,y) # plot
r <- sqrt(x*x+y*y) # distance to centre
rinside <- r[r<1] # inside circle with r=1?
n.inside <- length(rinside)
print(4*n.inside/n) # print pi estimation
}
The code is executed in R as follows:
> source("pirandom.R") # load the code (function) in the script
> pirandom(1000) # run the function for 1000 points
[1] 3.184 # 'pi' value estimation
